Электровыделение металлов

Зависимость электропроводности от температуры

Температурные коэффициенты электропроводности.

Термодинамика активации процесса электропроводности

В большинстве случаев электропроводность электролитных растворов — удельная и эквивалентная — экспоненциально зависит от обратной температуры:

— свободные (гиббсовы) энергии активации удельной

можно прогнозировать изменение удельной электропроводности от температуры.

определяется абсолютными величинами первого и второго слагаемых правой части уравнения (1—45).

Относительный температурный коэффициент удельной электропроводности находит Широкое применение в физико-химическом анализе жидких систем, поскольку диаграммы этого свойства позволяют с достаточной точностью определять стехиометрию продуктов присоединения.

Среди них наибольшее распространение получила теория переходного состояния (ТПС), основы которой были сформулированы Эйрингом. За последние годы эта концепция была распространена на транспортные процессы в растворах — вязкое течение, электропроводность, ионная миграция, диффузия. Однако при этом часто не учитывали условный характер представлений ТПС, вследствие чего полученные выводы не всегда оказываются физически обоснованными.

константы скорости процесса в ТПС

в принципе применимо для идеального газа. Переход к жидкой фазе требует учета коэффициентов активности в растворе, что в общем случае затруднительно, а при рассмотрении скорости транспортных процессов, особенно электропроводности в рамках данной теории, практически невыполнимо.

В рамках ТПС можно вывести уравнения для различных транспортных свойств, в частности для подвижности отдельного иона:

— весьма малая величина, и лишь предположительно считали ее равной единице. В последнее время М. И. Шахпаронов показал, что к не может быть больше 0,5.

.

С учетом этого обстоятельства в работе предложено следующее уравнение для предельной эквивалентной электропроводности:

В этих уравнениях величина предэкспоненциального множителя может быть рассчитана (для чего, очевидно, требуется знать легко находимую величину мольного объема индивидуального либо смешанного растворителя). С учетом числовых значений постоянных величин уравнение (1—48) преобразуется в выражение, позволяющее на основе экспериментальных данных рассчитывать свободную энергию активации ионной миграции при любой температуре, следовательно, энтальпию и энтропию этого транспортного процесса:

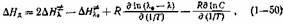
связывающее энтальпии равновесного и активационного процессов.

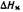раствора совпадает с таковой растворителя.

где

l— среднее расстояние перескока иона.

растворителя.

определяются выражениями

=—0,8733. Из уравнений (1—51) и (1—52) следует, что

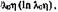поэтому представим выражение (1—54) в виде

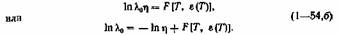
Продифференцировав (1— 54,а) по ЦТ, получим

— интегральные величины энтальпии активации ионной миграции и вязкого течения, находимые из уравнений

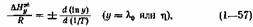
т. е. при постоянной е (рис. 15).

по выражению (1—44)

и по аналогичному экспоненциальному уравнению для вязкости, с одной стороны, и расчет этих величин на основе уравнений (1—51) и (1—52) —с другой, дают практически совпадающие результаты, так как величина

весьма мало изменяется с составом растворителя, и этим изменением можно пренебречь.

Универсальные растворители. В данном случае под универсальными растворителями будем понимать среды, для которых выполняется соотношение (1—38). В этом случае из выражений (1—55) и (1—38) следует

Выражение (1—53,а) с учетом уравнений (1—58) и (1—59) может быть представлено в виде

нелинейны и описываются по-

В этом случае уравнение (1—60) преобразуется к виду

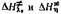как функции состава симбатны.

в я -алифатических спиртах (кДж/моль, 298 К)

а в

общем случае миграция ионов полностью описывается и определяется скоростью перескоков молекул растворителя в соседние положения равновесия и температурно-диэлектрическим влиянием среды.

, более информативны по сравнению с интегральной характеристикой, включающей по крайней мере три эффекта: температурные изменения подвижности ионов, вязкости и диэлектрической проницаемости.

неоправданно велики и по абсолютной величине, так как значительно превышают энергию теплового движения молекул растворителя.