Электровыделение металлов

Зависимость электропроводности от вязкости и диэлектрической проницаемости

Рассмотрим влияние указанных свойств растворителя на молекулярную (эквивалентную) электропроводность в разбавленных растворах электролитов (для концентрированных растворов данный вопрос рассмотрен в параграфе 1.3.2).

На протяжении многих десятилетий влияние вязкости растворителя на электропроводность описывается в литературе так называемым правилом Вальдена, согласно которому произведение предельной эквивалентной электропроводности данного электролита в различных растворителях есть величина постоянная:

Эмпирическое правило (1—34) получило впоследствии теоретическую трактовку, основывающуюся на гидродинамической теории, которая рассматривает ион как жесткую сферу, движущуюся в непрерывной изотропной среде. Радиус иона г в данном случае определяется уравнением Стокса — Эйнштейна:

— коэффициент диффузии. Коэффициент диффузии в бесконечно разбавленном растворе связан с подвижностью уравнением Нернста:

— заряд иона; F — постоянная Фарадея. Объединение уравнений (1—35), (1—36) приводит к выражению

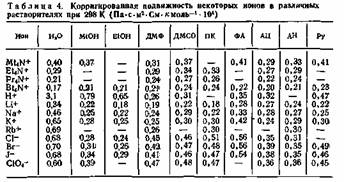
из которого следует, что при постоянстве r вальденовское произведение действительно должно сохраняться постоянным для данного иона в любом растворителе. Однако экспериментальные результаты по электропроводности неводных растворов показали, что правило (1—34) не соблюдается. В табл. 4 приведены величины вальденовского произведения для некоторых ионов. Как видно из данных таблицы, коррегированная подвижность не сохраняется постоянной даже для весьма объемистых тетраалкиламмо-нийных ионов.

обсуждалась в литературе и сводится в основном к постулированию факта об изменении

числа сольватации и эффективного ионного радиуса при переходе от одного растворителя к другому. Действительно, произведение радиуса сольватированного иона (см. параграф 1.4.1) на макровязкость растворителя и подвижность иона гораздо лучше сохраняет постоянство, чем вальденовское произведение. Предложено несколько эмпирических уравнений, связывающих ионный радиус с диэлектрической проницаемостью растворителя.

На эту зависимость впервые, по-видимому, указал А. М. Шкодин, однако уравнение (1—38) распространяется также на корригированные ионные подвижности. Пример, иллюстрирующий эту зависимость, приведен на рис. 14.

Применение принципа линейности свободных энергий ионной миграции и вязкого течения приводит к выводу о том, что для одного и того же электролита в ряду химически подобных растворителей либо в условно-универсальных средах хорошо соблюдается соотношение, учитывающее поправку величины корригированной электропроводности на мольный объем растворителя:

в случае индивидуального растворителя и псевдомольный объем в случае смешанного растворителя. Уравнение (1—39) можно представить в более общей форме:

наклона прямолинейной в случае универсальных либо условно универсальных сред зависимости свободной энергии активации вязкого течения от свободной энергии активации ионной миграции.

постоянна в интервале тем-

связать электропроводность растворов электролитов с электромагнитными свойствами растворителя.