Электровыделение металлов

Электропроводность двойных жидких систем

К двойным жидким системам относятся системы, образованные двумя жидкими при данной температуре компонентами. Системы, один из компонентов которых твердый при температуре исследования либо эксплуатации раствора, но хорошо растворяется во втором — жидком и образует концентрированные растворы, подчиняются большинству закономерностей, установленных для двойных жидких систем. Таким образом, излагаемый в этом параграфе материал несколько шире его названия.

К системам рассматриваемого типа относятся растворы галогенидов многих металлов III—VI групп периодической системы, т. е. достаточно широкий круг объектов.

Особенности кондуктометрии как метода физико-химического анализа рассмотрены в работах. Существующая классификация изотерм электропроводности основана на проводимости компонентов системы, а внутри каждого подраздела — на геометрии изотерм.

Системы, образованные не проводящими ток компонентами. Очевидно, что возникновение электропроводности в таких системах (точнее, электропроводности, на несколько порядков превышающей низкую электропроводность компонентов) в соответствии со схемой (1—14) однозначно свидетельствует о специфическом взаимодействии компонентов. На рис. 9, а приведены основные геометрические разновидности изотерм к данного класса систем. Несмотря на различие геометрии, все изотермы генетически связаны.

в таких системах в основном приходится на состав образующегося в системе соединения, минимум на изотерме и, в свою очередь, также может свидетельствовать о стехиометрии взаимодействия. Повышение температуры способствует понижению вязкости, что ведет к

сглаживанию минимума на изотермах и, в конце концов минимум исчезает, а изотерма и вырождается в кривую с одним максимумом — наиболее часто встречающуюся форму изотерм электропроводности двойных систем.

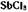— я-амиловый спирт диаграмма электропроводности которой приведена на рис. 9, б.

сохраняется лишь один максимум (правило М. И. Усановича уточнено в работе). Системы этого типа представляют наибольший интерес для практики электроосаждения металлов.

Системы, образованные компонентами, один из которых проводит ток в индивидуальном состоянии. Возможны четыре геометрических типа изотерм данного класса (рис. 10, а). Если в системах предыдущего класса возникновение электропроводности, существенно превышающей электропроводность компонентов, само по себе свидетельствует о химическом взаимодействии, то установление факта взаимодействия по кондуктометрическим данным Для систем данного класса требует учета ряда обстоятельств.

Рассмотрим прежде всего системы, где второй компонент является универсальным (индифферентным) растворителем по отношению к первому — электролиту.

В таких системах максимум на изотермах и появляется лишь в тех случаях, когда отношение вязкости электролита к вязкости растворителя весьма велико. Примером может служить система, диаграмма удельной электропроводности которой приведена на рис. 10,6.

Различие между системами с взаимодействием и без взаимодействия для рассматриваемого типа может быть установлено сопоставлением экспериментальных изотерм и с изотермами, рассчитанными в случае отсутствия специфического взаимодействия по уравнению:

с индексом А относятся к свойствам электролитного компонента; обозначения без индексов — к свойствам раствора; L — коэффициент пропорциональности, зависящий от соотношения диэлектрических проницаемостей компонентов.

В работе приведено более общее уравнение, связывающее свойства электролитного компонента со свойствами растворителя:

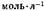), в котором величины постоянных определяются свойствами растворителя, а также микрофизическими характеристиками молекул растворителя и растворенного электролита и рассчитываются по формулам, приведённым в работе.

отвечающие изодиэлектрическим растворам в различных универсальных растворителях, не совпадают.

" в различных универ-

сальных растворителях.

и на аналитическую концентрацию серной кислоты. Как видно из рисунка, первому случаю, в отличие от второго, соответствует нормальный ход изотермы Я.